GAUSS ELIMINATION METHOD:EXPLANATION,ALGORITHM AND FLOWCHART

 Gauss elimination method

Gauss Elimination method can be adopted to find the solution of linear simultaneous equations arising in engineering problems. In the method, equations are solved by elimination procedure of the unknowns successively.

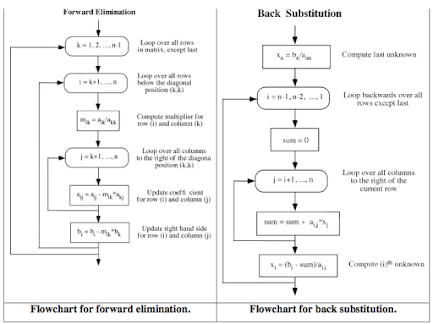
The method overall reduces the system of linear simultaneous equations to an upper triangular matrix. Then backward substitution is used to derive the unknowns. This is the key concept in writing an algorithm or program, or drawing a flowchart for Gauss Elimination.

Partial pivoting or complete pivoting can be adopted in Gauss Elimination method. So, this method is considered superior to the Gauss Jordan method.

In the Gauss Elimination method algorithm and flowchart given below, the elimination process is carried out until only one unknown remains in the last equation. It is straightforward to program, and partial pivoting can be used to control rounding errors.

Gauss Elimination Algorithm:

1. Start
2. Declare the variables and read the order of the matrix n.
3. Take the coefficients of the linear equation as:
   Do for k=1 to n
   Do for j=1 to n+1
   Read a[k][j]
   End for j
   End for k
4. Do for k=1 to n-1
   Do for i=k+1 to n
   Do for j=k+1 to n+1
   a[i][j] = a[i][j] – a[i][k] /a[k][k] * a[k][j]
   End for j
   End for i
   End for k
5. Compute x[n] = a[n][n+1]/a[n][n]
6. Do for k=n-1 to 1
   sum = 0
   Do for j=k+1 to n
   sum = sum + a[k][j] * x[j]
   End for j
   x[k] = 1/a[k][k] * (a[k][n+1] – sum)
   End for k
7. Display the result x[k]
8. Stop

FLOWCHART OF GAUSS ELIMINATION:

C PROGRAM FOR GAUSS ELIMINATION:

#include<stdio.h>

int main()

{

    int i,j,k,n;

    float A[20][20],c,x[10],sum=0.0;

    printf("\nEnter the order of matrix: ");

    scanf("%d",&n);

    printf("\nEnter the elements of augmented matrix row-wise:\n\n");

    for(i=1; i<=n; i++)

    {

        for(j=1; j<=(n+1); j++)

        {

            printf("A[%d][%d] : ", i,j);

            scanf("%f",&A[i][j]);

        }

    }

    for(j=1; j<=n; j++) /* loop for the generation of upper triangular matrix*/

    {

        for(i=1; i<=n; i++)

        {

            if(i>j)

            {

                c=A[i][j]/A[j][j];

                for(k=1; k<=n+1; k++)

                {

                    A[i][k]=A[i][k];

}

}

for(j=1; j<=n; j++) /* loop for the generation of upper triangular matrix*/

    {

        for(i=1; i<=n; i++)

        {

            if(i>j)

            {

                c=A[i][j]/A[j][j];

                for(k=1; k<=n+1; k++)

                {

                    A[i][k]=A[i][k]-c*A[j][k];

                }

            }

        }

    }

    x[n]=A[n][n+1]/A[n][n];

    /* this loop is for backward substitution*/

    for(i=n-1; i>=1; i--)

    {

        sum=0;

        for(j=i+1; j<=n; j++)

        {

            sum=sum+A[i][j]*x[j];

        }

        x[i]=(A[i][n+1]-sum)/A[i][i];

    }

    printf("\nThe solution is: \n");

    for(i=1; i<=n; i++)

    {

        printf("\nx%d=%f\t",i,x[i]); /* x1, x2, x3 are the required solutions*/

    }

    return(0);

}