GAUSS JORDAN METHOD:EXPLANATION,ALGORITHM AND EXPLANATION

 Gauss jordan method

Gauss Jordan method is commonly used to find the solution of linear simultaneous equations. In science and engineering, it is used to find the output of a chemical plant, examine a network under sinusoidal steady rate, etc.

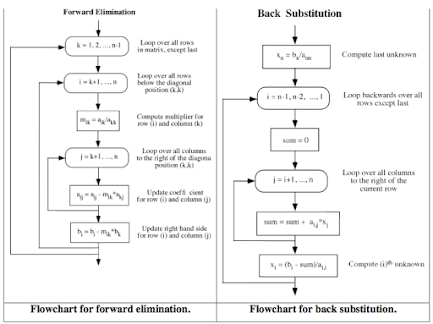
Here’s a simple algorithm for Gauss Jordan Method along with flowchart, which show how a system of linear equations is reduced to diagonal matrix form by elementary row operations. The solution is directly and conveniently obtained by this method but requires a little more calculation.

Gauss Jordan method is a modified version of the Gauss elimination method. The Gauss Jordan algorithm and flowchart is also similar in many aspects to the elimination method. Compared to the elimination method, this method reduces effort and time taken to perform back substitutions for finding the unknowns.

Gauss Jordan Method Algorithm:

  1. Start
  2. Read the order of the matrix ‘n’ and read the coefficients of the linear equations.
  3. Do for k=1 to n
    Do for l=k+1 to n+1
    a[k][l] = a[k][l] / a[k][k]
    End for l
    Set a[k][k] = 1
    Do for i=1 to n
    if (i not equal to k) then,
    Do for j=k+1 to n+1
    a[i][j] = a[i][j] – (a[k][j] * a[i][k])
    End for j
    End for i
  4. End for k
  5. Do for m=1 to n
    x[m] = a[m][n+1]
    Display x[m]
    End for m
  6. Stop

FLOWCHART:






C PROGRAM FOR GAUSS JORDAN METHOD:

#include<stdio.h>
int main()
{
    int i,j,k,n;
    float A[20][20],c,x[10];
    printf("\nEnter the size of matrix: ");
    scanf("%d",&n);
    printf("\nEnter the elements of augmented matrix row-wise:\n");
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=(n+1); j++)
        {
            printf(" A[%d][%d]:", i,j);
            scanf("%f",&A[i][j]);
        }
    }
    /* Now finding the elements of diagonal matrix */
    for(j=1; j<=n; j++)
    {
        for(i=1; i<=n; i++)
        {
            if(i!=j)
            {
                c=A[i][j]/A[j][j];
                for(k=1; k<=n+1; k++)
                {
A[i][k]=A[i][k]-c*A[j][k];
                }
            }
        }
    }
    printf("\nThe solution is:\n");
    for(i=1; i<=n; i++)
    {
        x[i]=A[i][n+1]/A[i][i];
        printf("\n x%d=%f\n",i,x[i]);
    }
    return(0);
}

Comments

Post a Comment

Popular posts from this blog

Newton Raphson Method:Explanation, algorithm and flowchart

 Newton raphson method: Newton-Raphson method, also known as the Newton’s Method, is the simplest and fastest approach to find the root of a function. It is an open bracket method and requires only one initial guess. The   C program for Newton Raphson method   presented here is a programming approach which can be used to find the real roots of not only a nonlinear function, but also those of algebraic and   transcendental equation s. Newton’s method is often used to improve the result or value of the root obtained from other methods. This method is more useful when the first derivative of f(x) is a large value. The programming effort for  Newton Raphson Method in C  language is relatively simple and fast. The convergence is the fastest of all the root finding methods discussed in  Numerical Methods Tutorial  section – the  bisection method , the  secant method  and the  regula-falsi method . Features of Newton Raphson Method: T...
Read more

GAUSS ELIMINATION METHOD:EXPLANATION,ALGORITHM AND FLOWCHART

Image
 Gauss elimination method Gauss Elimination method can be adopted to find the solution of linear simultaneous equations arising in engineering problems. In the method, equations are solved by elimination procedure of the unknowns successively. The method overall reduces the system of linear simultaneous equations to an upper triangular matrix. Then backward substitution is used to derive the unknowns. This is the key concept in writing an algorithm or program, or drawing a flowchart for Gauss Elimination. Partial pivoting or complete pivoting can be adopted in Gauss Elimination method. So, this method is considered superior to the  Gauss Jordan method . In the Gauss Elimination method algorithm and flowchart given below, the elimination process is carried out until only one unknown remains in the last equation. It is straightforward to program, and partial pivoting can be used to control rounding errors. Gauss Elimination Algorithm: Start Declare the variables and read the ord...
Read more

EULER METHOD:Explanation,algorithm,flowchart

Image
 EULER METHOD Euler’s method is considered to be one of the oldest and simplest methods to find the numerical solution of ordinary differential equation or the initial value problems. Here, a short and simple algorithm and flowchart for Euler’s method has been presented, which can be used to write program for the method in any high level programming language. Through Euler’s method, you can find a clear expression for y in terms of a finite number of elementary functions represented with x. The initial values of y and x are known, and for these an ordinary differential equation is considered. Euler’s Method Algorithm: Start Define function Get the values of x0, y0, h and xn *Here x0 and y0 are the initial conditions h is the interval xn is the required value n = (xn – x0)/h + 1 Start loop from i=1 to n y = y0 + h*f(x0,y0) x = x + h Print values of y0 and x0 Check if x < xn If yes, assign x0 = x and y0 = y If no, goto 9. End loop i Stop FLOWCHART OF EULER'S METHOD: C PROGRAM FOR ...
Read more